Solve by substitution 2x y = 5 3x 3y = 3 Solve the following system of equations by using the method of substitution 2x3y=9,quad 3x4y=5 We can substitute the expression for y given to us by the first equation into the second equation 5 = 4xy = 4x(3x5) = 4x3x5 = (43)x5 = x5 Then add 5 to both ends to get x = 10 Then substitute this value of x for x in the first equation y = 3x5 = 3*105 = 305 = 35Solve by substitution method x 2y = 1 and 2x 3y = 12 Get the answer to this question and access a vast question bank that is tailored for students
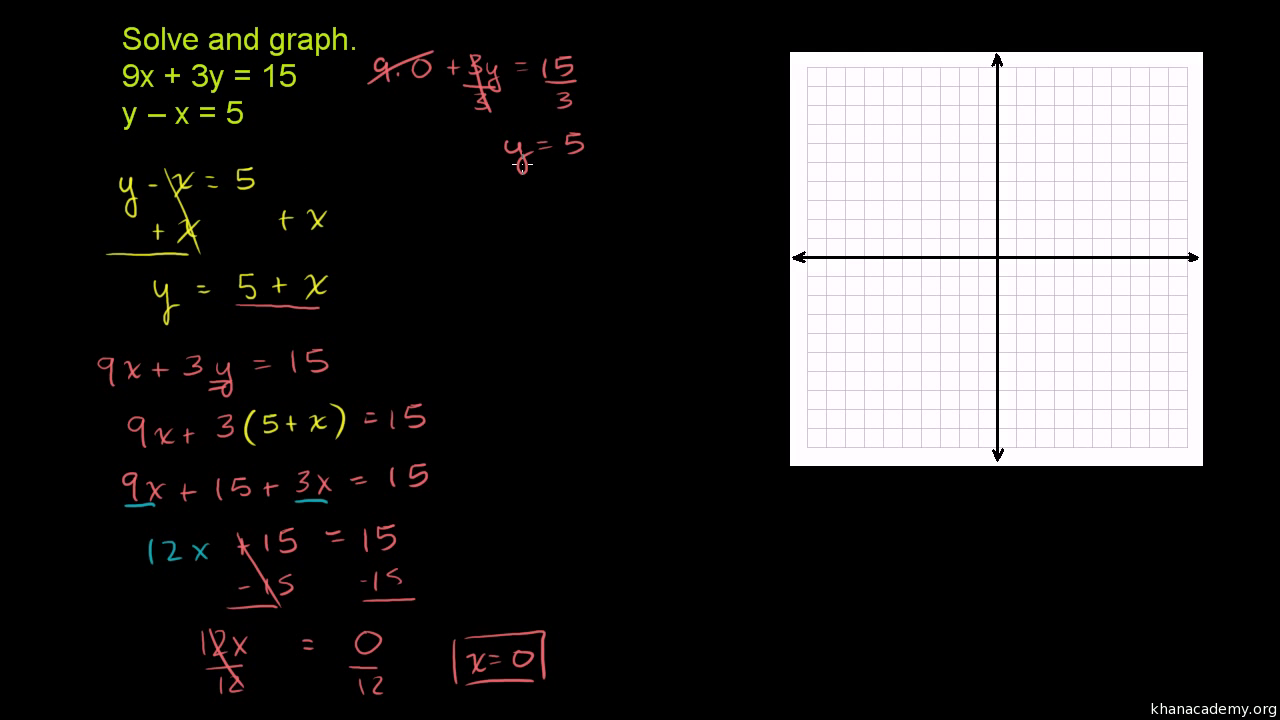
Systems Of Equations With Substitution 9x 3y 15 Y X 5 Video Khan Academy
5/x-3/y=1 3/2x 2/3y=5 by substitution method
5/x-3/y=1 3/2x 2/3y=5 by substitution method-Substitution Method xy = 5 and 2x3y = 4LinkedIn Profilehttps//wwwlinkedincom/in/arunmamidi8ba/FaceBookhttps//wwwfacebookcom/arunkumarm144View homework22pdf from MATH 990 at University of Utah MATH 990 Homework 22 Solve by the method of substitution 1 2xy=‐1 5 2x‐y=3 3x2y=5 5x3y=8 2 x‐y=2 6 x‐y=2




1 Graph The Following Equations A Y 3x 4 B 2x Chegg Com
Solve the system of equations by using the method of cross multiplication x 2y 1 = 0, 2x – 3y – 12 = 0 asked 6 days ago in Linear Equations by Hailley ( 260k points) linear equations in two variables 5/x3/y=1 3/2x2/3y=5Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreIf 5^2x3 × 3^3y7 = 225 Find x^2y^2 Disclaimer The questions posted on the site are solely user generated, Doubtnut has no ownership or control over the nature and content ofSolve the following equations by the method of inversion 5x y 4z = 5, 2x 3y 5z = 2, 5x 2y 6z = 1 0 Maharashtra State Board HSC Science (Computer Science) 12th Board Exam
Gujarat Board GSEB Solutions Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 35 Textbook Questions and Answers Gujarat Board Textbook Solutions Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 35 Question 1 Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutionsSolve by Substitution 2x3y=1 x3y=5 Subtract from both sides of the equation Replace all occurrences of with in each equation Tap for more steps Replace all occurrences of in with Simplify Tap for more steps Simplify each term TapSimple and best practice solution for 2x3y=3 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,
In this free online math video lesson on Solving Systems of Equations by Substitution we solve each system by substitution We Solve y=3x5 and 5x4y=3 byStep by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method 5x2y=3;y=2x Tiger Algebra Solver SOLVING SYSTEMS OF EQUATIONS ALGEBRAICALLY How to Use the Elimination Method How to Use the Substitution Method 97 2 x 1 5 x ≥ 0 4 4 4 Simplify both sides of the equation x=3 Substitute 3 in place of x in one of the original equations y = 2x y=2 3 y=6 The solution of the system is (3,6)Modeling Solve the following systems of equations by elimination




If 3x 2y 10 And 2x 3y 15 Find The Value Of X Y Youtube
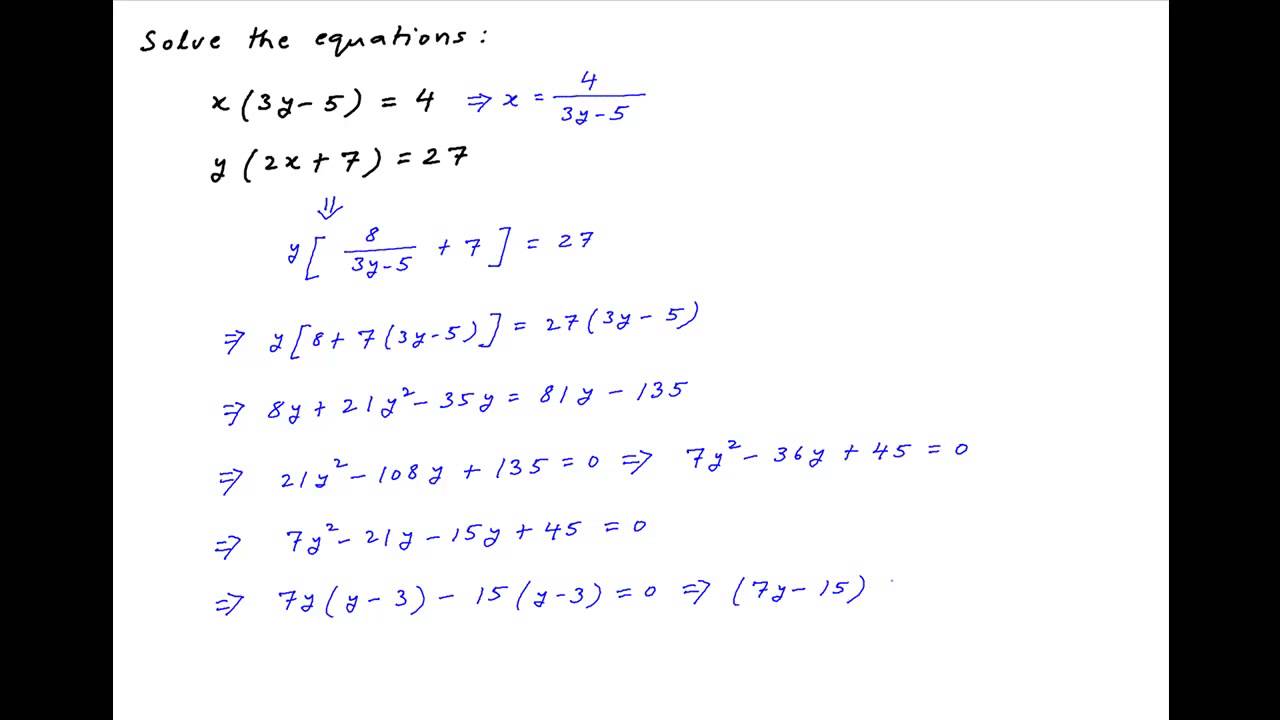



Solve The Equations X 3y 5 4 And Y 2x 7 27 Youtube
Step by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method 2x3y=1;y=x1 Tiger Algebra Solver We use the substitution method when we substitute numbers for variables in an algebraic expression or formula Substitution Method – Example Study the example below that shows how to use the substitution method in systems of equations Example Solve for x and y if 3x 2y = 4 and x 4y = 3 Answer x = 1 and y = 1/2 Step 1 Label theSolve each pair of equation by using the substitution method 2x3y=9 and 3x4y=5 Solve the following system of equations by using the method of substitution 2x3y=9,quad 3x4y=5 Solve (by any method) x 3y = 1 2x y = 3




Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 3



How To Expand X 3y 6 And Apply The Expansion To Evaluate 1 30 5 Correct To Five Decimal Places Quora
SOLVING SYSTEM OF EQUATIONS BY SUBSTITUTION The following steps will be useful to solve the systems of linear equations using substitution Step 1 In the given two equations, solve one of the equations either for x or y Step 2 Substitute the result of step 1 into other equation and solve for the second variable Step 3 Using the Substitution method solve 7x5y=23 6xy=25 Algebra Use the substitution method to solve x 3y=24 5x 8y=5 PreCalc Solve the system of equations using either the substitution method or the multiplication/addition method answer 3x2y=14 2x Ex 34, 1 (Elimination)Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 2 2(x y) = 2 × 5 2x 2y = 10 Solving




2 Use Cramer S Rule To Solve The Following Set Of Chegg Com




1 2 3x 4y 1 5 2x 3y 1 4 Amp 5 3x 4y 2 2x 3y 3 2 Problem Set 1 Q6 5 Youtube
1 Solve using the substitution method 3x y = 5 x 2y = 3 The xcoordinate is (Points 1) 7 2 1 2 2 Answered by a verified Math Tutor or TeacherSolve by Substitution 1/2x1/3y=5 , 1/4xy=10, Solve for Tap for more steps Simplify each equation Tap for more steps Combine and Simplify each term Tap for more steps Combine and Combine and Subtract from both sides of the equation Replace all 3/2x 2/3y = 5 , 5/x 3/y = 1 Answer only if you know it correctly Get the answers you need, now!




5x 3y 8 0 2x 3y 5 0 In Substitution Mothod Brainly In




5x 3y 8 0 2x 3y 5 0 In Substitution Mothod Brainly In
Solve the Following Pair of Linear (Simultaneous ) Equation Using Method of Elimination by Substitution 2( X 3 ) 3( Y 5 ) = 0 5( X 1 ) 4( Y 4 ) = 0Click here👆to get an answer to your question ️ Solve using the method of substitution 2x 3y = 7 ;👍 Correct answer to the question 5/x3/y=1 and 3/2x2/2y=5 by substitution method eanswersin
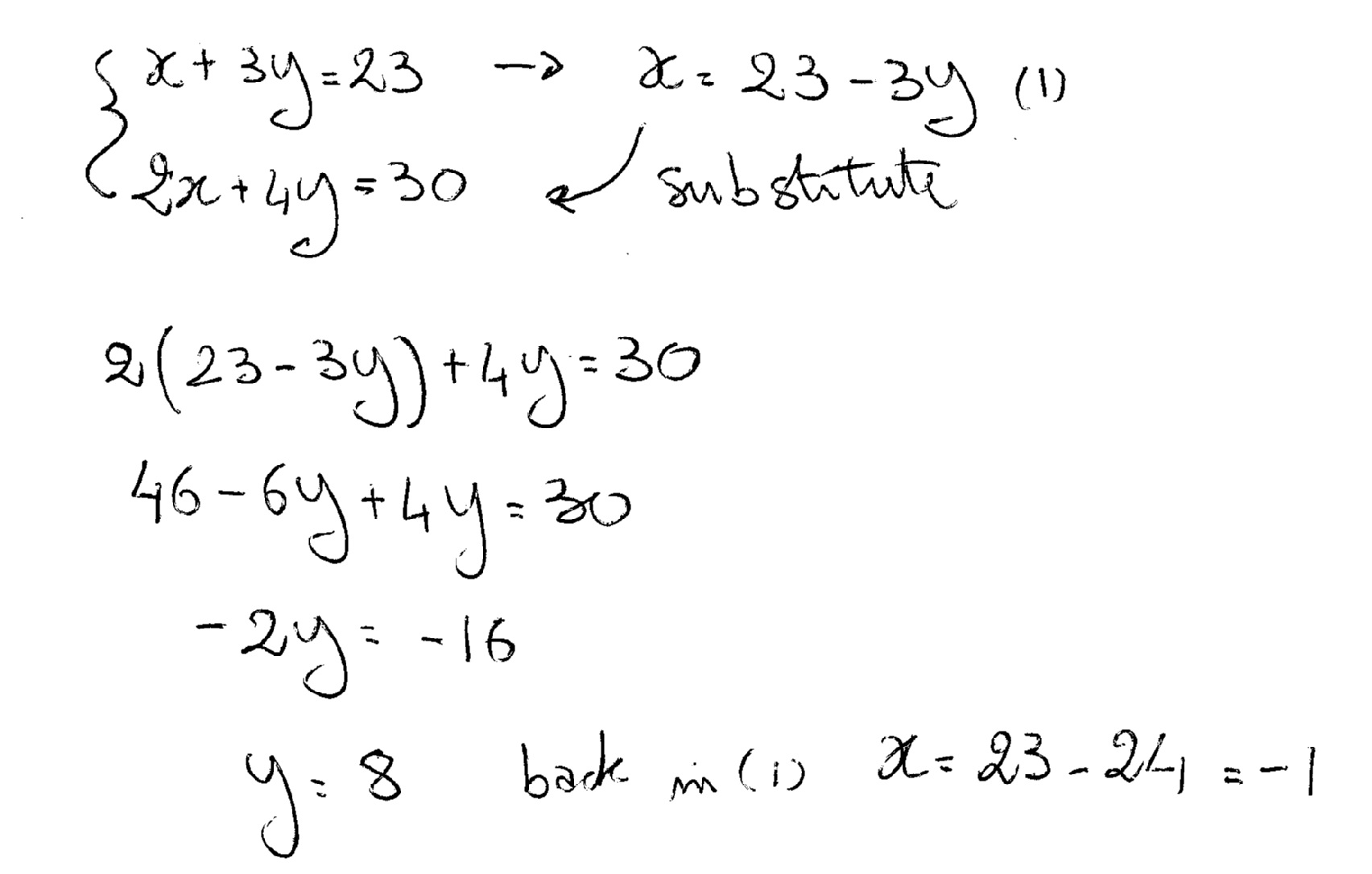



How Do You Solve By Substitution X 3y 23 And 2x 4y 30 Socratic




5 X 3 Y 1 3 2x 2 3y 5 Find The Value Of X Y By Substitution Method To Be A Brainliest Brainly In
Solving Systems Of Equations By Substitution Method In this method, we first find the value of one variable (y) in terms of another variable (x) from one equation Substitute this value of y in the second equation Second equation becomes a linear equation in x only and it can be solved for x Putting theSteps for Solving Linear Equation 2x3y = 5 2 x 3 y = 5 Subtract 3y from both sides Subtract 3 y from both sides 2x=53y 2 x = 5 − 3 y Divide both sides by 2 Divide both sides by 2Weekly Subscription $199 USD per week until cancelled Monthly Subscription $699 USD per month until cancelled Annual Subscription $2999 USD per year until cancelled




2 X 3 3 Y 5 0 5 X 1 4 Y 4 0 Solve It By Substitution Method Brainly In



Q Tbn And9gcsiggdhv5fw1mvrwy6npui8oe9vjy7ffnulpwxqmdm604bzyzap Usqp Cau
Transcript Ex 33, 1 Solve the following pair of linear equations by the substitution method (iv) 02x 03y = 13 04x 05y = 23 02x 03y = 13 04x 05y = 23 From (1) 02x 03y = 13 Multiplying both side by 10 (02x 03y ) ×10=13×10 2x 3y = 13 2x = 13 – 3y x = (𝟏𝟑 − 𝟑𝒚)/𝟐 Putting value of x in (2) 04x 05y = 23 04((13 − 3𝑦)/2) 05y = 23 Gujarat Board GSEB Solutions Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 34 Textbook Questions and Answers Gujarat Board Textbook Solutions Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 34 Question 1 Solve the following pair of linear equations by the elimination method and the substitution methodSolve the following pairs of linear equations (1 to 5) 1 (i) 2/x 2/3y = 1/6 2/x – 1/y = 1 (ii) 3/2x 2/3y = 5 5/x – 3/y = 1 Solution (i) 2/x 2/3y = 1/6 (1) 2/x – 1/y = 1 (2) By subtracting both the equations 5/3y = 5/6 By cross multiplication – 15y = 30 By division y = 30/ 15 = – 2 Substitute the value of




Solve The Following Simultaneous Linear Equation By Substitution Method 2x 3y 4 3 5x 2y 7 0 Brainly In




1 Solve The System Using Substitution Method 2x Y Chegg Com
x=1 y=2 You must make an equation that has only one variable in it so you can solve for that variable By finding the variable you can use it to find the other one Let's solve for y xy=3>y=3x substitute (3x) instead of y in x=3y5" " we get x=3(3x)5 x=93x5 4x=4 "x=1" Now we need to find y, we know that xy=3, and we know that x=1, so we substitute 1 instead of x xy=3>1y=3 "y=2"Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more#1 y=5x 3x4y= #2 x2y=6 2x3y=8 #3 3xy=1 x=2y5 #4 xy=6 y=32x #5 st=5 s=133t #6 xy=4 y=2x Algebra > Systemsofequations > SOLUTION Solve using the substitution method Algebra Systems of equations that are not linear Section




Which Of The Following Systems Has Equations That Are Dependent



Solve For X And Y 5 X 3 Y 1 3 2x 2 3y 5 Sarthaks Econnect Largest Online Education Community
X y=5 2x3y=5Question 1 Solve the following pair of linear equations by the elimination method and the substitution method (i) xy=5 and 2x 3y = 4 (i) 3x 4y = 10 and 2x 2y = 2 (iii) 3x 5y 4 0 and 9x = 2y 7Begin with 2x 3y = 5 Subtract 2x from each side3y = 5 2x Divide both sides by 3 y = 5/3 2x/3 Usually, you want to avoid leading your solutionRespuesta de 52 (1x)=2x3 Sumamos todos losThe following steps will be useful to solve system of linear equations using method of substitution Step 1 In the given two equations, solve one of the equations either for x or y Step 2 Substitute the result of step 1 into other equation and solve for the second variable Step 3 An example of a system of two linear equations is shown below We use a brace to show the two equations are grouped together to form a system of equations {2x y = 7 x − 2y = 6 A linear equation in two variables, such as 2x y = 7, has an infinite number of solutions Its graph is Find the number of students in each class QUse the method of substitution to solve each other




Solve The Following Pair Of Linear Equation By Substitution Method 2x 3y 19 And 3x 2y 21 Brainly In




Answered Exercise Set 9 1 S2y3d X 2y 7 Zx Bartleby
Solution Solution provided by AtoZmathcom Substitution Method Solve Linear Equation in Two Variables Solve linear equation in two variables 1 12x 5y = 7 and 2x 3y 5 = 0 2 x y = 2 and 2x 3y = 4 3 7y 2x 11 = 0 and 3x y 5 = 0 3x y = 5 > (2) Multiply equation (2) by 3 2x 3y = 7 9x3y = 15 _____ 11x = 22 Therefore x = 2 Substitute the x value in eqution (1) 2(2) 3y = 7 Therefore y = 1 The solution is x = 2 and y = 1 Now multiply equation (1) by 5 and (2) by 7 By adding both the equations Substitute the value of x in equation (1) Therefore, x = 7 and y = 2 If x = 7 and y – 2 satisfy the equation (3) then we can say that the equations hold simultaneously Substitute the value of x and y in equation (3) 43 = 43 which is true
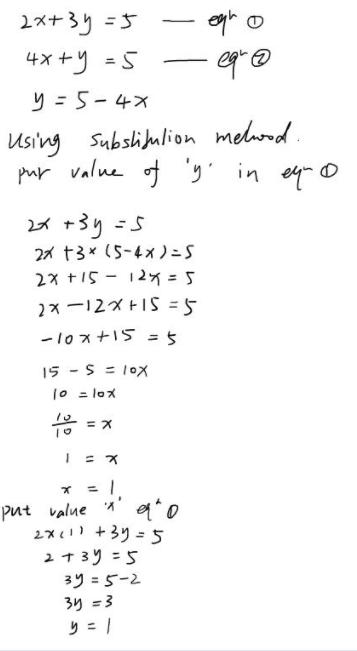



Solve The Following System Of Equations Using The Method Of Substitution 2x 3y 5 4x Y 5 Snapsolve




Ch 3 5 Elimination Multiplication Ppt Download
Next Post Next Change to slopeintercept form Then find the yintercept, first point, and second point x 3y > 9 slope intercept form y Intercept first2) Plug in the value of that variable into the other equation and solve for the one variable left 3) Plug that value into 1 and solve for the first variable Since step one has already been done for us we can just jump to step to 2y x = 3 x = 3y 5 Plugging x = 3y5 into the top equation you get 2y (3y5) = 3 now we just solve for y 2y Now, after getting the equation in terms of x or y now, solve the equation either for x or for y Put (3) in equation (1) 2x 3y = 9 2 (3 y) 3y = 9 6 2y 3y = 9 5y = 9 – 6 5y = 3 Y = 3/5 After getting a solution for one variable, now use the substitution method You have to put the value of the variable in equation one you find




1 Use The Substitution Method To Solve Each Linea Gauthmath




2 3 Y 5 Buy Clothes Shoes Online
Solve the following systems of simultaneous linear equations by the substitution method (1 to 4) 1 (i) x y = 14 x – y = 4 (ii) s – t = 3 s/3 t/2 = 6 (iii) 2x 3y = 9 3x 4y = 5 (iv) 3x – 5y = 4 9x – 2y = 7 Solution (i) x y = 14 x – y = 4 It can be written as x = 4 y By substituting the value in the above equation 4 yClick here👆to get an answer to your question ️ Solve the equation by substitution method 2x 3y = 9 , 3x 4y = 55x y = 9




Systems Of Equations With Substitution 9x 3y 15 Y X 5 Video Khan Academy




Solve The Following Pair Of Linear Equations By The Elimination Method And The Substitution Method X Y 5 And 2x 3y 4
Find an answer to your question By substitution method x2y=1 and 2x3y=12 saurockzz5785 saurockzz5785 Math Secondary School answered • expert verified By substitution method x2y=1 and 2x3y=12 2 See answers Vishank Vishank Answer Stepby




最も好ましい 5 X 3 Y 1 3 2x 2 3y 5 By Substitution Method Nyosspixyjla



How To Find The Equation Of A Straight Line Through The Point Of Intersection Of Lines 2x 3y 5 0 And 3x 4y 7 0 Which Is Perpendicular To The Line 5x 3y 2 0 Quora




If The System Of Equations 2x 3y 5 4x K Y 10 Has Infinitely Many Solutions Then Youtube




2x 3y 4 0 3x Y 5 0 Youtube




Solve The Following Pair Of Linear Equations By Substitution Method 2x 3y 19 And 3x 2y 21



Www Shaalaa Com Question Bank Solutions Solve X Y 5 X 3 Y 1 3 2x 2 3y 5 Pair Linear Equations Two Variables




1 Graph The Following Equations A Y 3x 4 B 2x Chegg Com




2x 3y 1 0 7 4x 3 Y Youtube




Solve By Elimination Method X Y 5 2x 3y 5 Brainly In



Solve The Following Systems Of Equations 1 7x 1 6y 3 1 2x 1 3y 5 Sarthaks Econnect Largest Online Education Community




X 2y 5 2x 3y 10 Solve By Substitution Method Brainly In
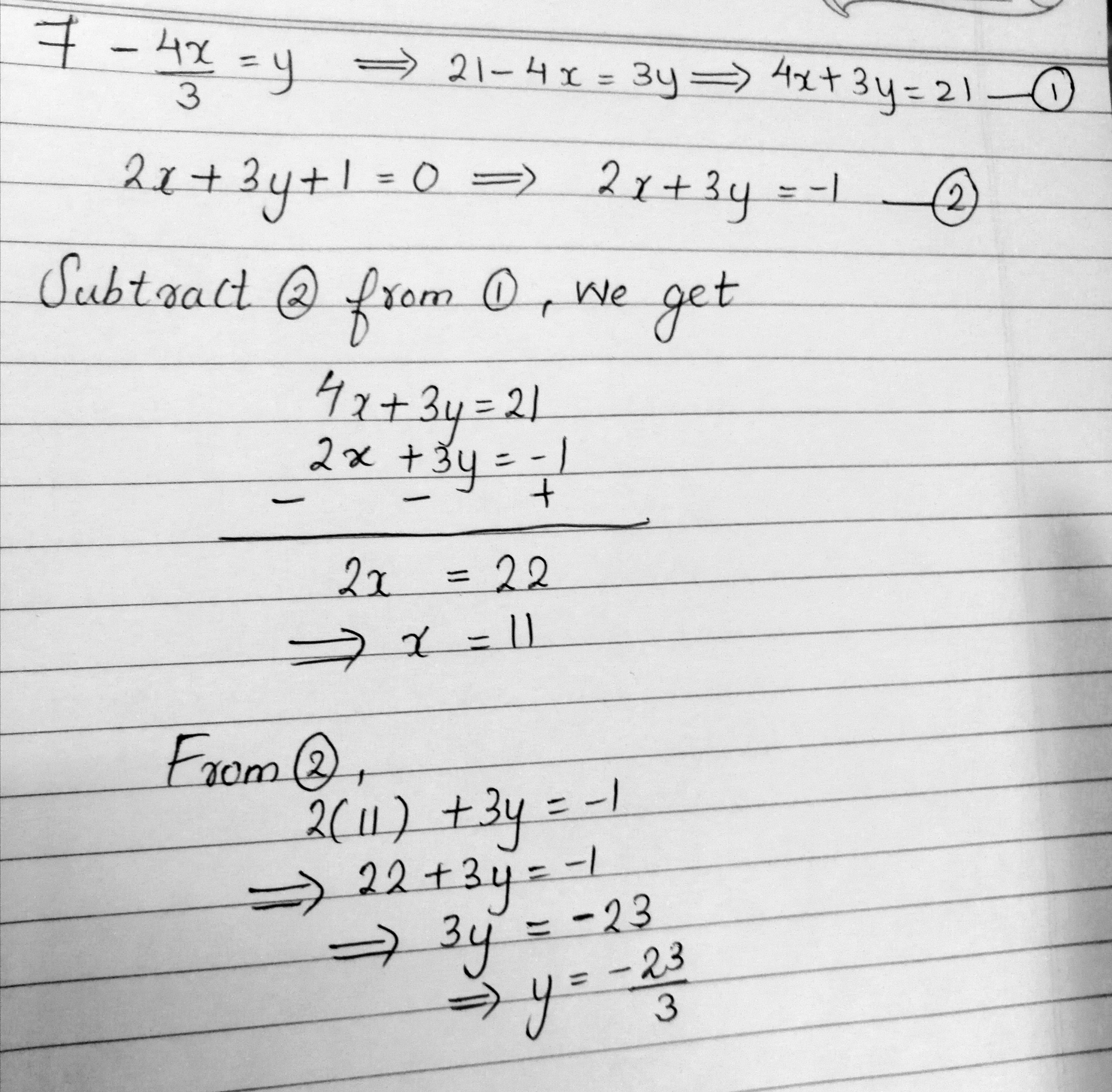



7 4x 3 Y 2x 3y 1 0 Mathematics Topperlearning Com Iwb1egg




3x Y 2 0 2x 3y 5 0 By Substitution Method Brainly In



2 3 Y 5 Buy Clothes Shoes Online




X 3y 5 3x Y 5 Brainly In




7x 3y 1 0




1 Solve The Following Systems Of Linear Equations Chegg Com




3 2x 2 3y 5 5 X 3 Y 1 Solve For X And Y Youtube




3x 5y 11 X 3y 1 Do Now Homework Solutions 2 2x 2y 6 Y 2x 2x 2 2x 6 2x 4x 6 6x 6 X 1y 2x Y 2 1 Y Ppt Download




Systems Of Equations Substitution Method Ppt Video Online Download




2x 3y 5 0 And 3x 2y 12 0 Find The Solution Using Substitution Method Brainly In




最も好ましい 5 X 3 Y 1 3 2x 2 3y 5 By Substitution Method Nyosspixyjla



The Substitution Method




2 Y 3 Y 4 Buy Clothes Shoes Online




Solve The System 2x 3y 5 3x 2y 4 Youtube




3 58 Solve The System By Using The Elimination Chegg Com




What Is The Solution For An Equation Of A Line Passing Through The Point Of Intersection Of 2x 3y 5 0 And 7x 5y 2 0 And Parallel To The Lines 2x 3y 14 0 Quora




Graph Graph Inequalities With Step By Step Math Problem Solver



Systems Of Linear Equations
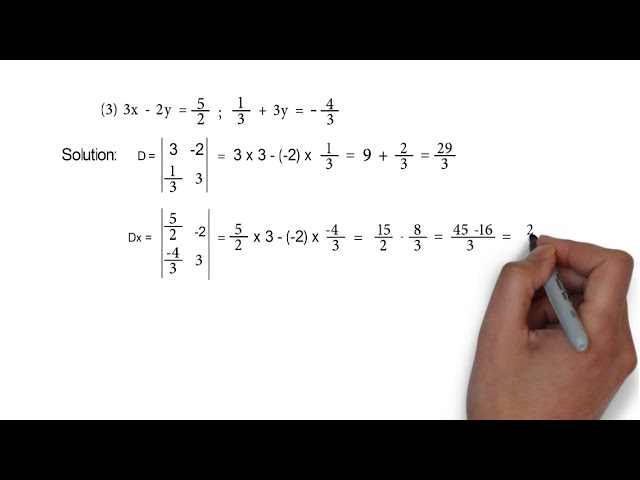



3x 2y 5 2 And 1 3 3y 4 3 Problem Set 1 Q5 3 Linear Equation In Two Variables Youtube




6 2 Solving Systems Of Linear Equations 455 We Have Chegg Com
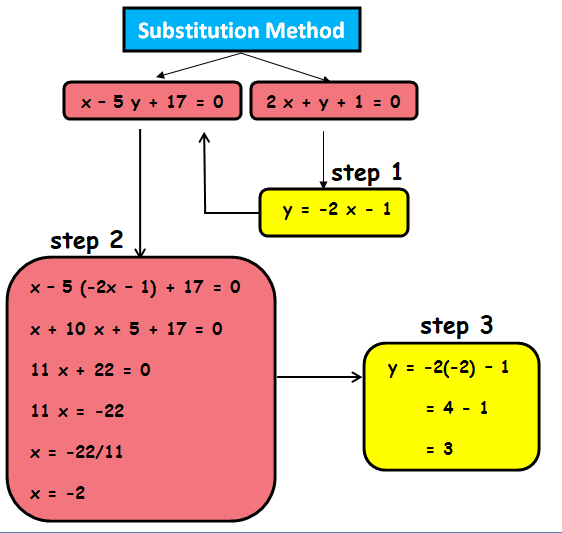



Substitution Method Examples




3x 4y 10 4x 3y 5 Youtube



What Is The Answer Of 2x Y 3 7x 3y 4 Using Gauss Elimination Method Quora
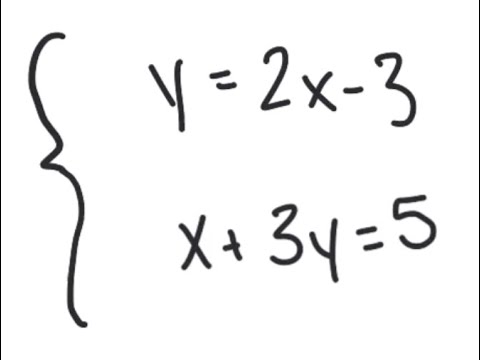



Substitution Solve The System Y 2x 3 X 3y 5 Youtube




What Is The Solution For An Equation Of A Line Passing Through The Point Of Intersection Of 2x 3y 5 0 And 7x 5y 2 0 And Parallel To The Lines 2x 3y 14 0 Quora




J19




What Is The Solution For An Equation Of A Line Passing Through The Point Of Intersection Of 2x 3y 5 0 And 7x 5y 2 0 And Parallel To The Lines 2x 3y 14 0 Quora




Systems Of Equations With Substitution 9x 3y 15 Y X 5 Video Khan Academy




最も好ましい 5 X 3 Y 1 3 2x 2 3y 5 By Substitution Method Nyosspixyjla
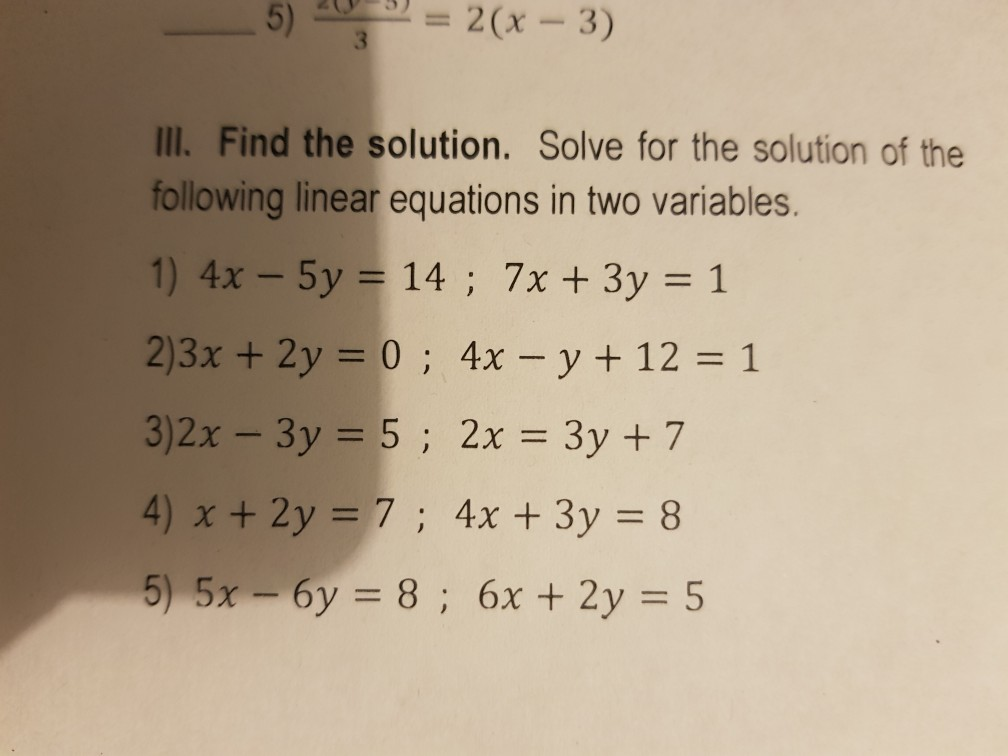



7x 3y 1 0




Solve The Following Linear Equation By Substitution Method 8x 3y 12 5x 2y 7




2x 3y 5 X 2y 3 0 How To Solve This Problem With Elimination Method Brainly In




By Elimination Method Solve 3 2x 2 3y 5 5 X 3 Y 1 Brainly In




Show Graphically That The System Of Linear Equations 2x 3y 5 6y 4x 3 Youtube




Ex 3 4 1 I Class 10 Solve By Elimination And Substitution




1 Solve By The Addition Method 5x 3y 26 2x 2y Chegg Com
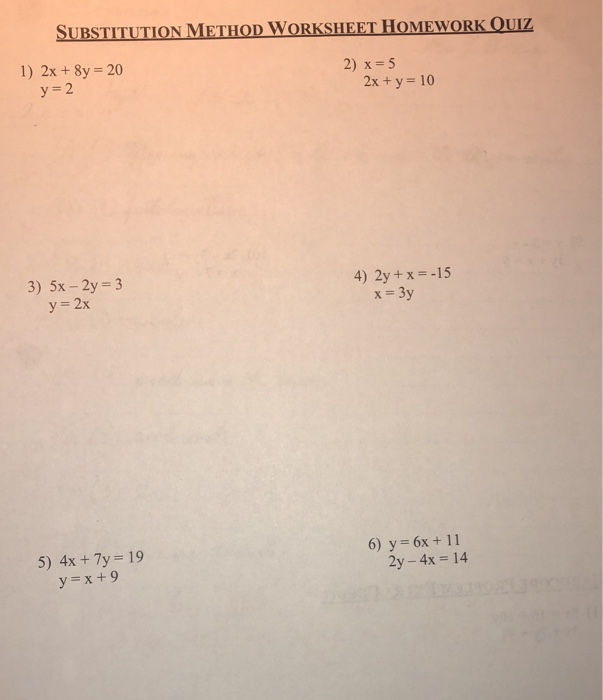



Substitution Method Worksheet Homework Ouiz 1 2x 8y Chegg Com




Ex 4 6 3 Examine Consistency X 3y 5 2x 6y 8 Ex 4 6




Solve The Following Simultaneous Equation By Elimination Method 3x 4y 10 4x 3y 5




Answers




3 Systems Of Linear Equations




Solving A System Of Equations Using A Matrix Precalculus Socratic




What Is The Point Of Intersection In The Lines Of 2x 3y 10 And 3x 2y 5 Quora




2 3 Y 5 Buy Clothes Shoes Online




Solving A System Of Equations Using A Matrix Precalculus Socratic




1 Use The Substitution Method To Solve Each Linea Gauthmath




Solve For X And Y 1 7x 1 6y 3 1 2x 1 3y 5 Brainly In



1



Mfm2p



1
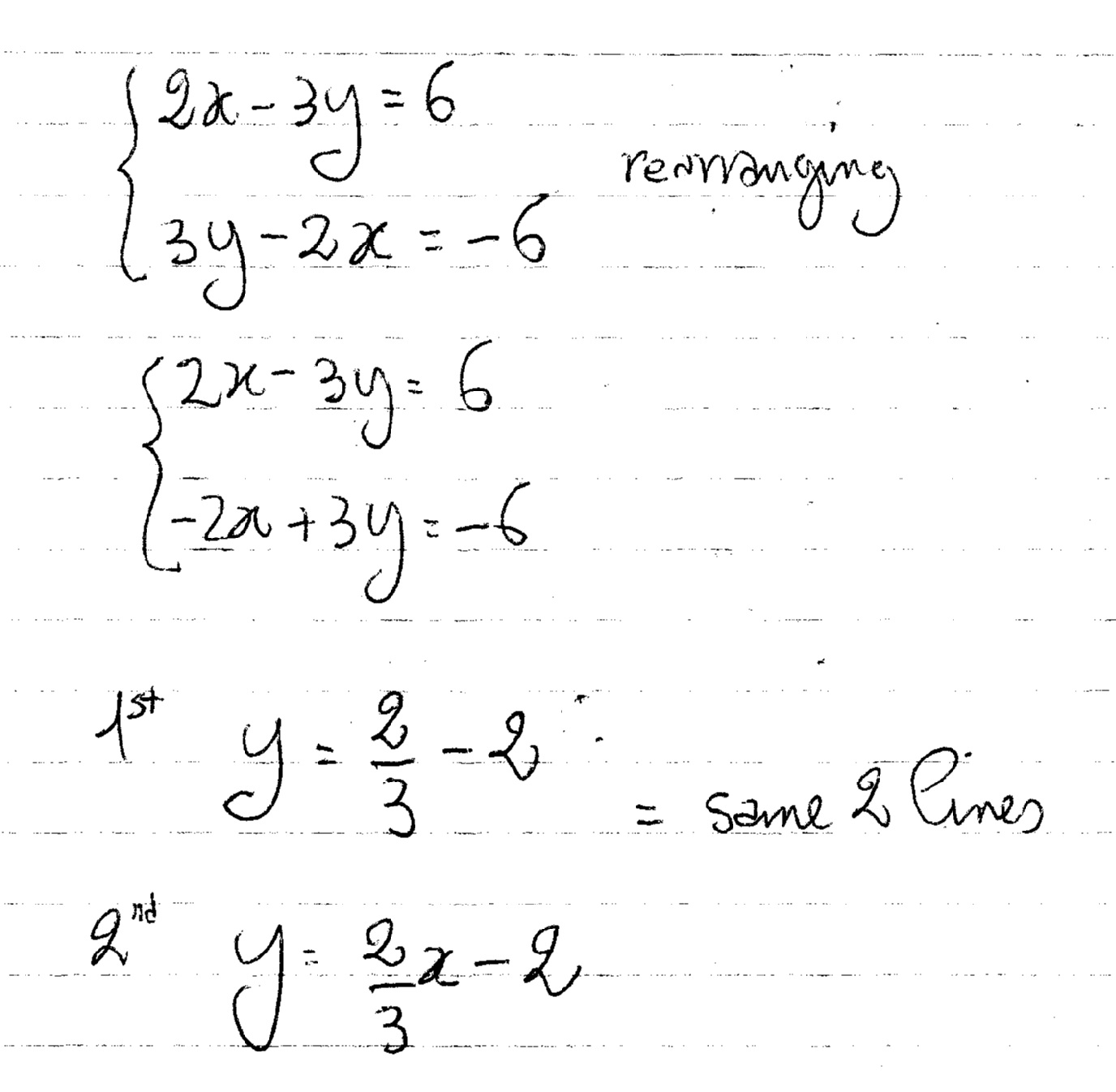



How Do You Solve The System Of Equations 2x 3y 6 And 3y 2x 6 Socratic




If 3x 5y 9 And 5x 3y 7 Then Find The Value Of X Y Youtube
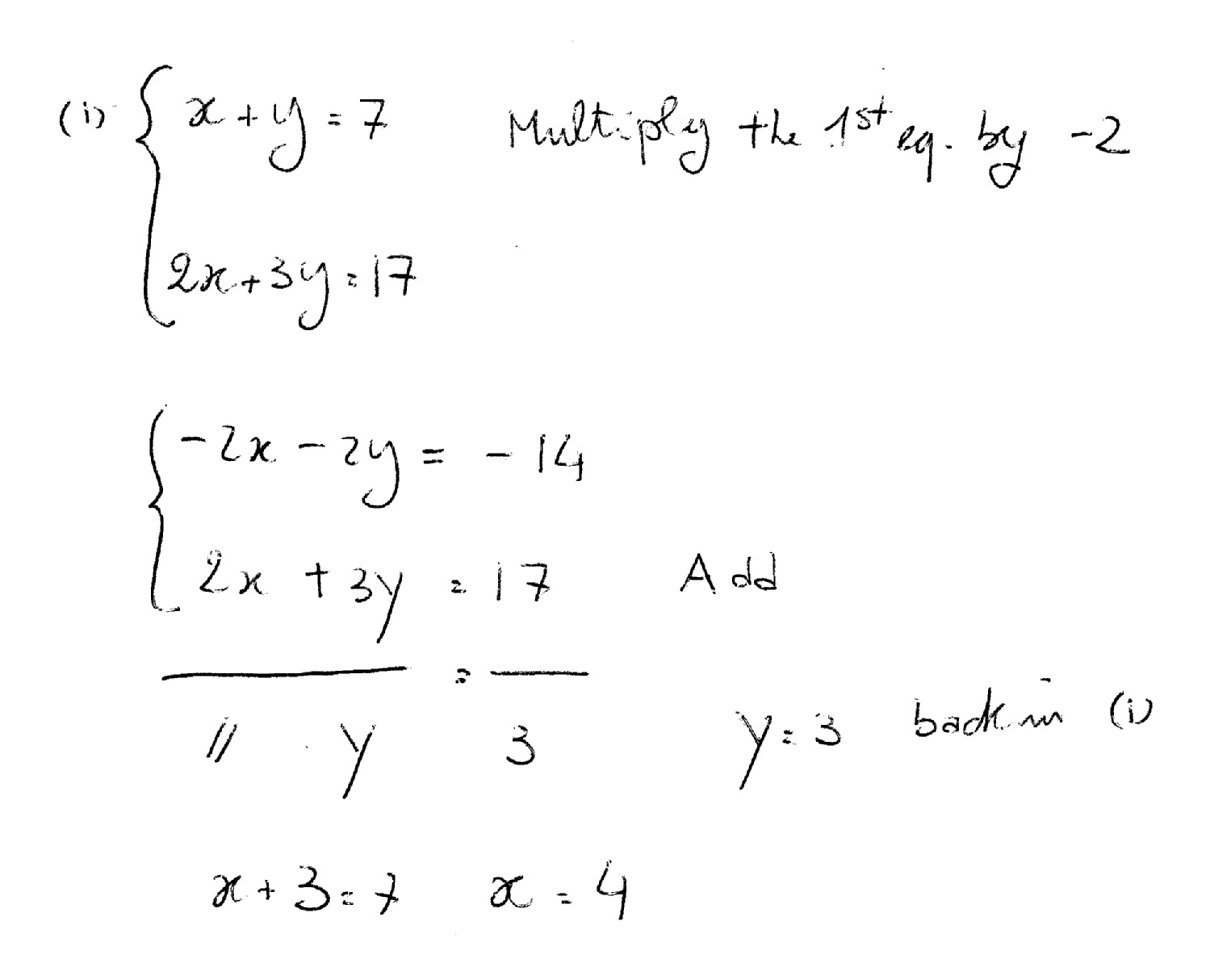



How Do You Solve The System Using The Elimination Method For X Y 7 And 2x 3y 17 Socratic




Show That The System Of Equations 2x 5y 17 5x 3y 14 Has A Unique Solution Find The Solution
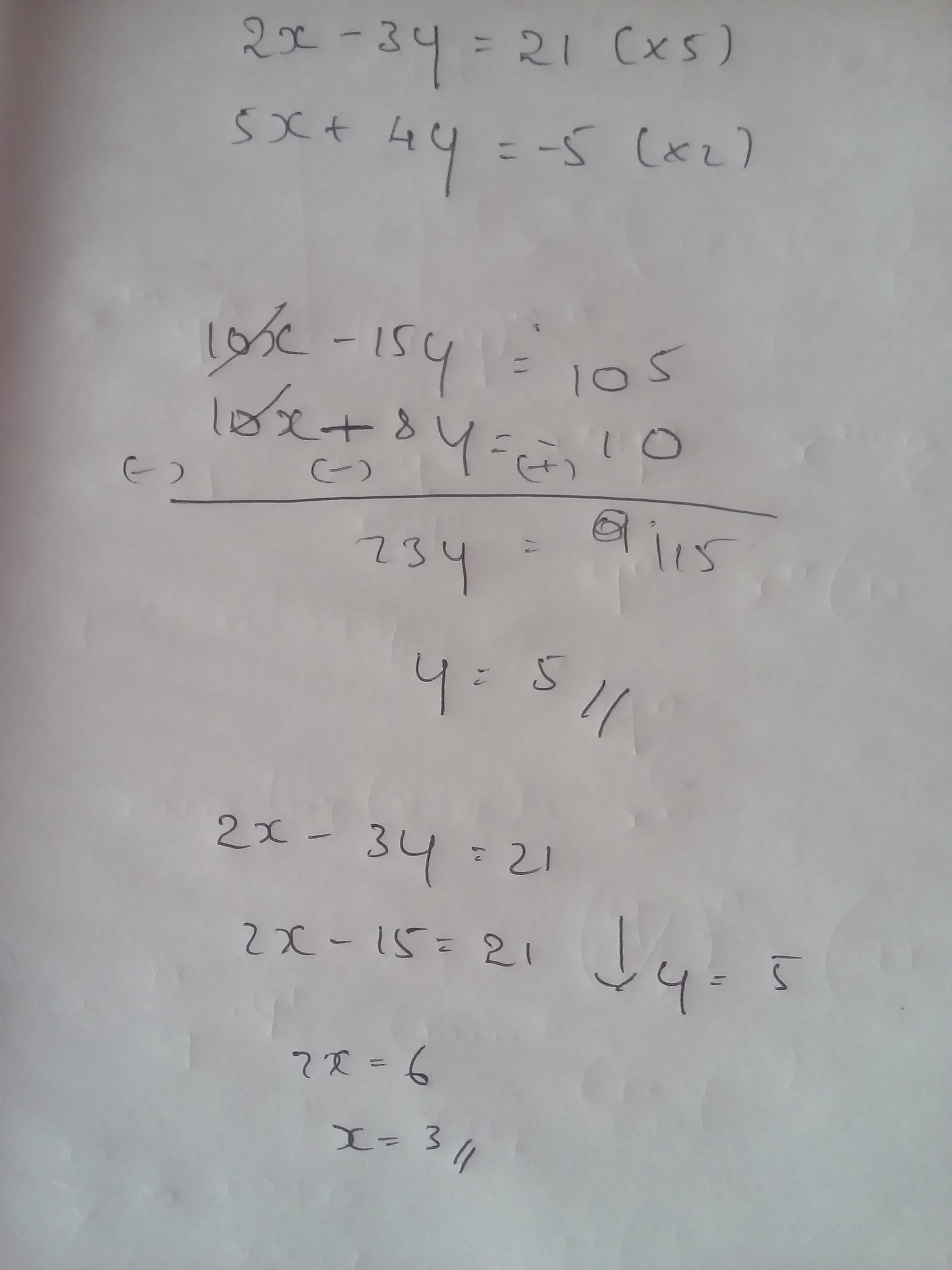



How Do You Solve 2x 3y 21 And 5x 4y 5 Socratic




5 X 3 Y 1 3 2x 2 3y 5 Brainly In




In The Following System Of Equation Determine Whether The System Has A Unique Solution No Solution Or Infinitely Many Solution In Case There Is A Unique Solution Find It 2x 3y
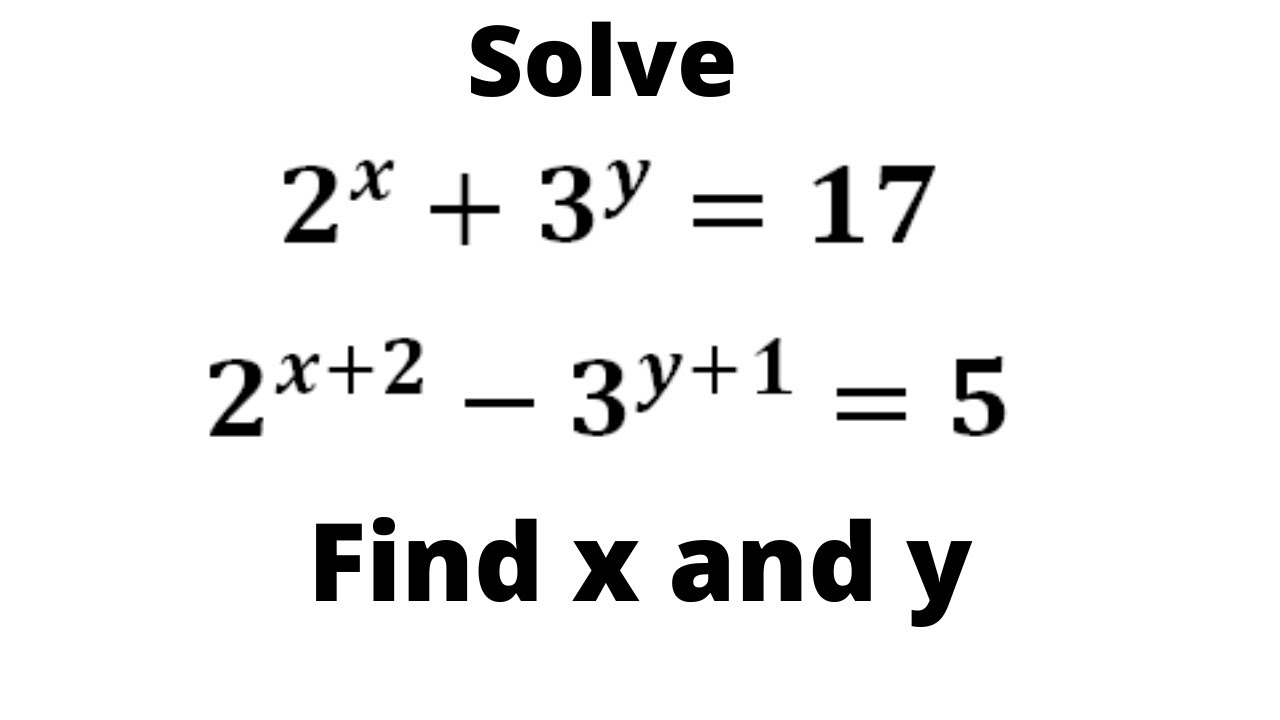



Solve 2 X 3 Y 17 2 X 2 3 Y 1 5 Find X And Y Youtube




Let S Learn Solving Systems Using The Substitution Method




Practice Solving Systems By Graphing 1 2 2x 5y 5 X 3y Ppt Download




5x 3y 1 2x 5y 19 Solve It By The Method Of Substitution Need Answer With Full Method No Brainly In




3x 2 5y 3 2 And X 3 Y 2 13 6 Solve Using Substitution Method Youtube




Find The Solution Of The Differential Equation By The Chegg Com
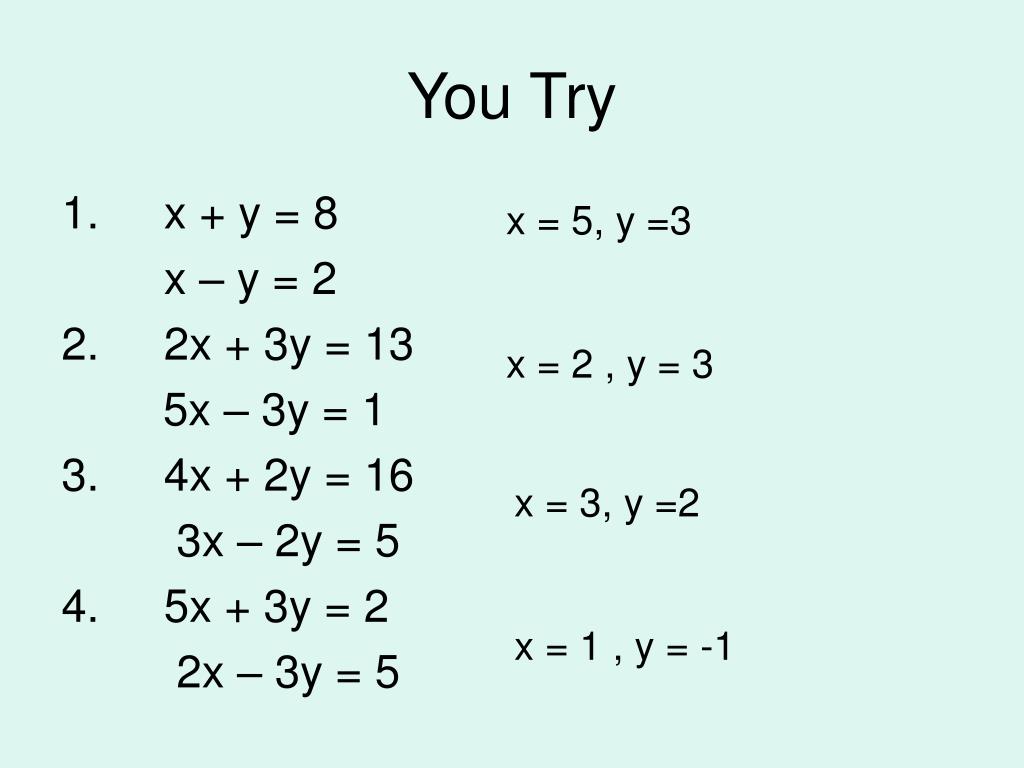



最も好ましい 5 X 3 Y 1 3 2x 2 3y 5 By Substitution Method Nyosspixyjla




21 Solve The Linear Equations 2x Y 5 And 3x 2y 1 Using Substitution Method22 Check Whether 150 Is A Brainly In



If X 3y 1 3 Y What Is Dy Dx At The Point 2 8




1 Solve The System Using Substitution Method 2x Chegg Com




Solve By Using Substitution Method 2x 3y 2 X Chegg Com




2x 2y 2 X 3y 7 Solve By Substitution Youtube


